Range versus Output

Three statistics measure how well a water gun performs: output, the rate at which water shoots from the nozzle; shot time, the duration of the blast; and range, the distance the stream covers. To simiplify matters, the power statistics are solely range and output; shot time must decrease to increase power.

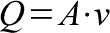
Output is a deceptively simple statistic--it measures how quickly water leaves the soaker. The equation for volumetric flow demonstrates that output increases as the flow area and speed of the stream increase: for instance, a large bucket can have a very high flow rate without high speed. The flow area is large because the bucket is large. A filled bucket, when inverted, should easily achieve a gallon per second, or about 128 ounces per second.

Range, on the other hand, is very difficult to achieve. Output varies from the standard 1 ounce per second to the immense 800 ounces per second from Ben's SuperCannon II; range varies little from the standard 30 feet to the not-so-immense 73 feet from Ben's SuperCannon II. Why is it that SuperCannon II has 800 times the standard in output yet its range is only twice the standard? Output does not require much work, but range does. There are no simple equations to analyze range. The prediction of output uses many quantities, but the prediction of range uses many qualities at this point. Two factors seem to affect range the most though: how powerful the gun is and the how cohesive the stream is.

Stream Cohesion

Straight power will increase range to a certain extent. Weak guns consequently achieve bad ranges. Too much power without the proper increases in cohesion and laminar flow will limit the overall range of the gun. Do runners flail their arms crazily while running to get extra speed? In running, good form is important. In water gunning, this form is stream cohesion.

Stream cohesion measures how well a stream stays together. A less cohesive stream will break up before its potential is met. All of the power in world can be dumped into powering a gun, but if the stream breaks apart early on water will go nowhere. The more cohesive a stream has, the less effective drag is on it.

When properly formed, the flow in a gun will be laminar, having no erratic changes in velocity. Laminar flow maximizes the use of the power of the system. The opposite of laminar flow is turbulent flow, and for the most part bends create this turbulence. Flow tends to follow streamlines. From this, the most effective method to create a laminar design is to create a linear design with a straight path from the chamber to the nozzle, avoiding rapid changes in the diameter of the piping, as they too create turbulence. Conical nozzles allow the flow to gradually come together to cohere more.

Of all the parts on a water gun, the most important for good stream cohesion is the nozzle. The nozzle shapes and forms the stream before it leaves the gun. A good barrel on firearm will be the right length, and a good nozzle on a water gun will be the correct size. Like optimal barrel length, each water gun has an optimal nozzle size. The size of the orifice manipulates the stream speed and cohesion as shown by the volumetric flow rate equation. The larger the area, the larger the stream will be, which makes it more resistant to drag. The smaller the area, the higher the speed will be.

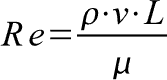
The accepted practice of measuring turbulence is with the Reynold's number. The dimensionless number is the ratio of the inertial forces to the viscous forces. In laminar flow, the viscous forces dominate, forcing the number below 2300. Slower flow stays together better, but since speed is more or less a measure of power, we do not slow our flow down. Smaller diameters also increase laminar flow. The flow can better follow lines when forced through a smaller, linear pipe. The mesh screens and linear guidance walls (straws) work on this principle. The overall flow is maintained while laminar flow is increased. Each straw divides the flow to condition it.

Calculation of Range

To be blunt, range is hard to calculate. As said before, there is no equation relating range and other quantities. However, there is a general equation to deal with the motion of fluids.

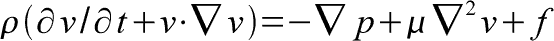
The Navier-Stokes Equations are some of the most useful ever conceived, as they can accurately predict all kinds of phenomena, including water flow in pipes and possibly the flow of liquids in gases (as a solution for range would need). However, they are above most people, being differential equations and not algebraic equations. The equations are, nonetheless, the ones we would need to use to truly predict fluid flow in water guns and midair flow. Bernoulli's equation does not work for viscous flows like water. The algebraic methods currently used are not accurate enough to truly predict or approach the accuracy that gradients and partial derivatives would achieve.

Good design and practice in water guns should improve their ranges. Principles like linear design and conical nozzles should help. Without the practice of good design, much energy will be wasted to achieve mediocre results.