Super Soaker Central

The pump shaft diameter in a separate pressure chamber gun directly affects the gun's performance. A pump shaft's area is dictated by its diameter. The wider the shaft, the more water is pumped in each stroke. However, more force is needed to complete a stroke.

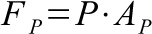
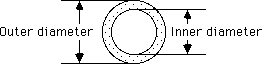
The area of the pump is the inner area of the pipe, the area of a circle with the diameter of the pipe's inner diameter.

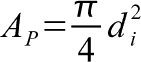
The force required to complete a stroke is a function of the pressure (P) in the pressure chamber as well as a function of the area of pump shaft (Ap). Within the pressure chamber, the pressure powering the gun is transmitted through the water; fluids carry pressures. However, when the gun is not being pumped, the pressure is not transmitted past the second check valve leading to the pump. Once the pump is on a return stroke though, the pressure is transmitted to the pump shaft and a user would feel the force needed to pump the gun.

But how does a wider pump shaft require more force to pump? Isn't the user putting more energy into the chamber than with a smaller pump shaft? No, the energy is the same for a given pump volume.

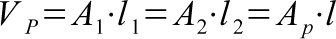
In physics, work or energy is equal to force by distance. In this case, the force is the pumping force and the distance is distance required for each pump. To provide a correct comparison, the same pump volume must be used. The pump shaft area by the length of the stroke equals this set quantity.

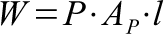
Substituting in the force equation, the work required is a function of three variables. However, A*L equals the pump volume V. Substituting in V for volume, the work for required to pump remains the same for a set displacement in volume, regardless of variations in diameter and length. Energy is conserved; in wider diameter pumps, the stroke length is shorter, allowing the energy to remain the same for each pump volume.

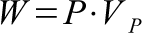
In the end, wider pumps require more force to pump but also pump more water.

v