Basic Equations
Written by Drenchenator
Last updated on 2007-07-26
Basic Equations
Foreword
I wrote this article to outline some basic equations that describe the physics behind water guns. Most are basic, requiring algebra; the rest are advanced, requiring calculus. Nevertheless, these equations form other more advanced ones.
Variables and Units
| Statistic | Variable | Metric | Customary | Soakerdom |
| Pressure | P | Pa, atm | psi, psig | psig |
| Volume | V | L,mL | oz, gal | L, mL, oz, gal |
| Output | Q | L/s, mL/s | oz/s, GPM | oz/s, mL/s, L/s |
| Time | t | sec | sec | sec |
| Force | F | N | lb | lb |
| Area | A | cm^2, mm^2 | in^2, ft^2 | - |
| Distance | r, x | mm, cm, m | in, ft | ft, m |
| Velocity | v | m/s | fps, mph | - |
| Quantity | n | - | - | - |
Pressure
Pressure is force per unit area. For our purposes, gases apply pressure; liquids do not compress unless subjected to forces unattainable by our means. By far, the most common unit for pressure is pounds per square inch (psi or PSI), though other common units include atmospheres (atm) and pascals (Pa).
Unlike force, pressure is not a vector value because it is applied equally in all directions. Pressure is measured using two systems: absolute pressure and gauge pressure. Gauge pressure is the pressure displayed on a pressure gauge, the pressure difference between absolute pressure and atmospheric pressure. Absolute pressure adds atmospheric pressure to gauge pressure.
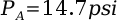
An important constant deals with absolute pressure: the pressure of the atmosphere. Atmospheric pressure equals exactly 1 atm and approximately 14.7 psi.
Boyle's Law
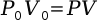
When temperature stabalizes, Boyle's Law idealizes the relationship between a gas' pressure and its volume. If volume decreases, pressure increases. If volume increases, pressure decreases. This equation is incredibly useful in gas systems because it models pressure as volume changes or volume as pressure changes.
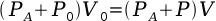
Note: Boyle's Law uses absolute pressure and applies only to gases.
Volume
Water Volume after Pumps
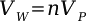
The volume of water pumped in the pressure chambers after a certain number of pumps is easy to calculate. As long as each stroke is full, the amount of water inputed into the any gun's chamber is the product of the number of pumps and the volume of water moved in each stroke.
Total Chamber Volume
Calculations involving pressure often involve the total volume of the pressure chamber. This volume differs from the volume of water shot out, because some air occupies the chamber at all times. The first equation finds the volume of a cylinder, the second the volume of a sphere.
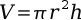
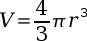
Many times the shape of the chamber is irregular but has circular cross sections. If a radius equation can be defined, the volume can be found using the next equation. This equation computes the volume of any region with circular cross sections.
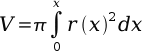
A much easier method to calculate the total volume involves disassembling the soaker. The disconnected pressure chamber is filled with water and the volume of water measured with a graduated cylinder or scale.
Air Pressure Soakers

In a standard air pressure water gun, the pressure chamber has a set total volume. With both air and water occupying the chamber, the sum of the volume of air and water matches the entire chamber's volume. Pressure relates to output using this equation, Boyle's Law, and the calculus definition of output.
Output
Output is the rate at which water shoots out of a water gun. In fluid mechanics, output is known as volume rate of flow. The units are in volume per unit of time. Common units for rate of flow include liters per second (L/s) and gallons per minute (GPM). By far the most common unit for output in water gunning is the X system. 1x signifies 1 ounce per second. The X system was based on the output of the XP 70, which approximates 1 ounce per second. In fluid mechanics, the variable for rate of flow is a capital Q.
Output is measured inconsistently in water gunning. Many describe output as the amount of water emitted during the first second of the shot. This method does not describe the shot as a whole because output is greatest at the beginning of a shot. For instance, air pressure guns have severe output dropoff. Average output is the other common measure of output. The total water emitted is divided by the time taken. Many times, the shot does not last for an entire second or water shoots out at a significantly greater rate at the beginning of the shot. Average output depicts the shot as a whole.
Real Life Examples
| Device | mL/s | oz/s | L/s | GPM |
| SS 50 | 10 | .33 | .01 | .16 |
| XP 70 | 30 | 1 | .03 | .48 |
| Garden hose with nozzle | 105 | 3.5 | .105 | 1.66 |
| Flash Flood riot blast | 360 | 12 | .36 | 5.71 |
| CPS 2000 | 900 | 30 | .9 | 14.27 |
| Air Pressure Homemade | 1500 | 50 | 1.5 | 23.78 |
| SuperCAP | 3560 | 120 | 3.56 | 56.433 |
| Fire hose | 4000 | 133 | 4 | 63.41 |
| Supercannon II | > 15000 | > 500 | > 15 | > 250 |
| Police riot control water cannon | 15000 | 500 | 15 | 250 |
| Water usage in a steam engine | 18900 | 631 | 18.9 | 300 |
| Low Flow Fire Hydrant | 47300 | 1577 | 47.3 | 750 |
| Center Pivot Irrigation | 63000 | 2130 | 63 | 1000 |
| Modern Gravity Irrigation | 76000 | 2560 | 76 | 1200 |
| High Flow Fire Hydrant | 94600 | 3154 | 94.6 | 1500 |
Relationship to Volume
By definition, output is the rate at which water leaves the soaker and pressure chamber as well. This point is often overlooked. Output is directed related to the amount of water in the gun.
Volume Flow Rate
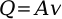
This equation is known as the volumetric flow rate equation. In water gunning, it calculates stream velocity at the nozzle. Using the area of nozzle and the output rate, the stream exit velocity can be calculated.
Average Output
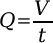
As described earlier, average output is the volume of water shot out divided by the shot time.
Instantaneous Output
Like any other rate, output can change over time. While average output shows the average rate over an interval, instantaneous output tells the exact rate at a certain time.
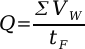
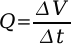

Starting with the equation for average output, a change in the volume of water over a change in time is equal to the average output. Basic calculus then allows the equation to be rewritten in instantaneous terms (Q=dV/dt).
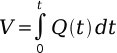
The true connection between output and volume of water in the chamber can now be defined. Treated as a differential equation and solved for V, the volume of water shot out of a soaker can be calculated.